|
Authors:Béla Weissa,∗, Zsófia Clemensb, Róbert Bódizsc,d, Zsuzsanna Vágóa, Péter Halásza aFaculty of Information Technology, Pázmány Péter Catholic University, Práter u. 50/a, 1083 Budapest, Hungary ∗ Corresponding author. Tel.: +36 1 886 4759; fax: +36 1 886 4724. Article history: Received 21 May 2009 AbstractFractality is a common property in nature. It can also be observed in time series representing dynamics of complex processes. Therefore fractal analysis could be a useful tool to describe the dynamics of brain electrical activities in physiological and pathological conditions. In this study, we carried out a spatio- temporal analysis of monofractal and multifractal properties of whole-night sleep EEG recordings. We estimated the Hurst exponent (H) and the range of fractal spectra (dD) in 10 healthy subjects. We found higher H values during NREM4 compared to NREM2 and REM in all electrodes. Measure dD showed an opposite trend. Differences of H and dD between NREM2 and REM reached significancy at circumscribed regions only. Our results contribute to a deeper understanding of the fractal nature of brain electrical activities and may have implications for automatic classification of sleep stages Keywords: EEG Sleep stages, Self-similarity, Monofractal analysis, Hurst exponent, Multifractal analysis, Generalized dimensions, Fractal spectrum 1. IntroductionVarious objects in dead and living nature show the so-called self-similarity (SS) or fractal property (Mandelbrot, 1982). In the geometrical sense the SS property means that a self-similar geometric object (fractal) shows at least an approximately similar pattern at different scales, i.e., it possesses scale-invariant properties that can be characterized by a single scaling exponent. This is also termed monofractal (MOF) property. A geometrical multifractal (MUF) is a non-uniform, more complex fractal. Unlike a uniform monofractal it exhibits local density fluctuations and it can be decomposed into many sub-sets characterized by different exponents (Tel and Vicsek, 1987; Jestczemski and Sernetz, 1996). Fractal property can also be interpreted from the functional aspect. It can be observed in time series representing dynamics of complex systems as well. Fractal time series can be characterized by long-range temporal correlations, their scale-free power-law characteristics indicate that fluctuations over brief times are proportional to those measured over a longer period (Beran, 1994; Kantz and Schreiber, 2003). SS properties of the geometry and activity of the brain have also been discovered. Lowen et al. revealed that individual ion channel currents show long-term correlation and possess SS properties (Lowenet al., 1999).Considering spike trains inextracellular recordings long-termcorrelations were found among interspike intervals of medullary sympathetic neurons in cats (Lewis et al., 2001). Spasic et al. showed that fractal dimension of local field potentials of anaesthetized rats changes significantly after unilateral discrete injury (Spasic et al., 2005). Intracranial electroencephalogram (IEEG) and scalp EEG recordings are considered as top of the brain electrical activity hierarchy and emerge from field potentials through brain structures also showing fractal properties (Pellionisz, 1989; Kiselev et al., 2003). Therefore, SS properties of these recordings can be conjectured. Recently it was suggested that fractal analysis of IEEG signals could be used in epilepsy research to detect and perhaps to predict focal seizures (Osorio and Frei, 2007; Weiss et al., 2008a,b). In a psychophysiological study emotional involvement during task performance was also shown to be reflected in fractal properties of the EEG (Kulish et al., 2006). We expected that spatio-temporal MOF and MUF analysis of EEG signals provide useful information about the dynamics of brain electrical activity during different vigilance states as well. For a recent review of nonlinear EEG analysis under physiological and pathological conditions including sleep we refer to Stam (2005). Fractal properties of the human sleep EEG have already been investigated by other research groups (Pereda et al., 1998; Shen et al., 2003; Lee et al., 2004; Acharya et al., 2005;Ma et al., 2006; Leistedt et al., 2007a,b), however, these studies were limited by low sampling rate (100 Hz in Acharya et al., 2005; Ma et al., 2006; Leistedt et al., 2007a,b; 128Hz in Shen et al., 2003) or low number of EEG channels (Fpz-Cz and Pz-Cz in Acharya et al., 2005;Ma et al., 2006; Cz in Leistedt et al., 2007a,b; C3 in Pereda et al., 1998; Shen et al., 2003;C4in Lee et al., 2004). To assess MOF properties Pereda et al. (1998) estimated the fractal exponent β using coarse grain spectral analysis. The scaling exponent α of detrended fluctuation analysis (DFA) was applied in Shen et al. (2003), Lee et al. (2004), and Leistedt et al. (2007a,b), while in Acharya et al. (2005) the authors used the SS exponent H.In Shen et al. (2003), Lee et al. (2004), and Leistedt et al. (2007b), the α exponent showed consistently higher values for deep NREM compared to light NREM and REM, while no such relation was observed in Acharya et al. (2005) for H, although H is linearly related to α (Kantz and Schreiber, 2003). Pereda et al. (1998) also found higher β values for deeper sleep stages. Ma et al. (2006) assessed MUF properties of the sleep EEG estimating the range of the singularity strength and the asymmetry of the singularity spectrum. These measures also correlated with the sleep depth, exhibiting higher v alues for deeper sleep stages. Although each of these studies reported significant differences, five studies (Shen et al., 2003; Lee et al., 2004; Acharya et al., 2005; Leistedt et al., 2007a,b) were limited to describing significant main effects. Pereda et al. (1998) compared only stage NREM4 with other stages and only one study (Ma et al., 2006) revealed significant differences for all pairs of the assessed vigilance states. It is to be noted that none of the abovementioned studies assessed topographic aspects of the temporal fractal properties. Moreover, as far as we know, no previous study carried out a joint analysis of MOF and MUF properties in sleep recordings. Therefore, here our aim was to perform a spatio-temporal analysis of MOF and MUF properties using wholenight multichannel scalp EEG recordings to characterize the fractal behaviour of the human sleep EEG. 2. Materials and methods2.1. Subjects and EEG recordingsTen healthy subjects with no sleep disturbances, free of drugs and medications as assessed by an interview and questionnaires on sleeping habits and health participated in the study (age: 17–53 years, mean ± S.D.: 30 ± 10.1 years, five males and five females). The study was approved by the ethical committee of the Semmelweis University and subjects gave written informed consent to participation. Sleep was recorded in the sleep laboratory for two consecutive nights. The timing of lights off was determined by the subjects, and morning awakenings were spontaneous. On average subjects spent 475.3 ± 72 min (mean ± S.D.) in sleep. Sleep was recorded by standard polysomnography, including electroencephalography (Fp1, Fp2, F3, F4, Fz, F7, F8, C3, C4, Cz, P3, P4, T3, T4, T5, T6, O1 and O2 electrodes), electrooculography (EOG), bipolar submental electromyography (EMG) and electrocardiography (ECG). EEG electrodes were referenced to the contralateral mastoid. Midline EEG electrodes were referenced to the right mastoid. Impedance of the EEG electrodeswas kept below5 kω. Signals were collected, pre-filtered, amplified and digitized at a sampling rate of 249Hz/channel using the 30 channel Flat Style SLEEP La Mont Headbox with implemented second order filters at 0.5 Hz (high pass) and 70Hz (low pass) as well as the HBX32-SLP 32 channel preamplifier (La Mont Medical Inc., USA). Additionally, a 50 Hz digital notch filtering was performed by means of the DataLab acquisition software (Medcare, Iceland). 2.2. EEG processingMonofractal and multifractal properties of the whole-night EEG recordings were evaluated by estimation of the SS parameter H(also called Hurst exponent or Hurst parameter) and the range of fractal spectra (dD), respectively. To estimate H, we applied the rescaled adjusted range based approach, while dD was approximated by estimation of the generalized dimensions spectra. Because of the non-stationary properties of EEG signals and the presence of artefacts raw EEG data were first pre-processed. The detailed description of the applied methods can be found below. Signal processing was accomplished using an EEG visualization and processing toolbox under Matlab2007b (MathWorks, Natick,MA, USA) and statistical analysis was performed in STATISTICA (StatSoft, Inc., Tulsa, OK, USA). 2.2.1. Pre-processingAlthough hardware filtering had been applied during EEG recording, some artefacts remained. Thus, we first performed software filtering on the raw EEG recordings with Butterworth IIR filters (eight order 0.3–70 Hz band-pass and 50 Hz notch with a quality factor Q= 45). To avoid phase distortion,we used the built-in filtfilt() function of the Matlab for zero-phase digital filtering. H and dD were estimated for the whole-night sleep recordings using short data segments because of the non-stationary property of EEG signals. Estimation of nonlinear measures from time series of finite length is accompanied by doubt (Hu et al., 2001; Kantz and Schreiber, 2003). Therefore, the selection of the optimal segment length for estimation of these measures is always a trade-off between the goodness of estimation (longer segments are required formore accurate estimations) and capturing brief perturbations in time series (shorter segments are needed because of the non-stationarity). Based on our preliminary analysis and previous studies we set the segment length to 20 s. High temporal resolution of the estimated values was achieved using 19 s overlap For all subjects a hypnogram was prepared according to the Rechtschaffen and Kales standard (Rechtschaffen and Kales, 1968) using 20 s long epochs. To compare fractal properties during different sleep stages 90 epochs of 20 s length were selected from sleep stages NREM2, NREM4 and REM (30min/stage) for all subjects. Selection included segments without artefact contamination only. Due to immense artefacts during waking this vigilance state could not be statistically addressed in the present study. 2.2.2. Estimation of HThe stochastic process X(t) with continuous parameter t is self- similar with the self-similarity parameter H if the distribution of the rescaled process c−HX(ct) is the same as the distribution of X(t), where c > 0 is arbitrary (Mandelbrot and Taqqu, 1979). H is widely used to assess monofractality, scale-free properties and the degree of long-range temporal correlations of time series.When 0 < H < 0.5, an increase in the process is more probably followed by a decrease and vice versa, the process is considered to have short-range dependence. If H= 0.5, observations of the process are uncorrelated. When 0.5 <H< 1, an increase in the process is more probably followed by an increase and a decrease ismore probably followed by a decrease, the process is considered to have long-range dependence (Beran, 1994; Kantz and Schreiber, 2003; Acharya et al., 2005). For the estimation of H we implemented the rescaled adjusted range or R/S statistics based method (Mandelbrot and Taqqu, 1979; Beran, 1994) in order to compare our results with those presented in Acharya et al. (2005), Osorio and Frei (2007), and Weiss et al. (2008b). Comparison of different approaches to estimate the H parameter of electrical brain activities can be found in (Osorio and Frei, 2007). Here we summarize only the R/S statistics based method briefly. Let X(n) be a discrete time series. The partial sumprocess is defined as
The sample variance of the process X can be obtained using
The adjusted range is given by
where
The R/S statistics or the rescaled adjusted range is defined by
In Mandelbrot and Taqqu (1979) it was proven that for self-similar processes the expected value of R/S(n) is proportional to nH, i.e.
as n→∞,where CH is a positive constant and H is the self-similarity parameter of the process. Using this power-law relationship the Hurst exponent can be estimated by:
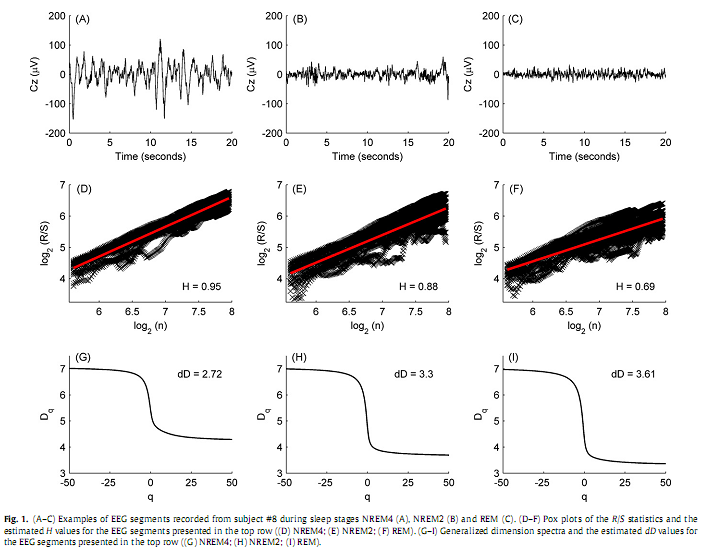
To estimate H, the N sample point long data segments (N=20×249 = 4980) were subdivided into K blocks (K = 20). Blocks of length N/K corresponded to duration of 1 second. R/S(n) was computed starting at points kl = lN/K +1, l =0, 1,…, K−1. These values canbedenoted by R(kl ,n)/S(kl ,n).Overlapping of blocks was avoided, the upper boundary, i.e., the high cut-off point (hcf =249) of n was limited to N/K. This resulted K different estimates of R(n)/S(n) for each value of lag n. By plotting log[R(kl ,n)/S(kl ,n)] versus log(n)we got the so-called pox plot for the R/S statistics. H can be estimated by fitting a straight line to the points in this plot. It is equal to the slope of the fitted line. Pox plots for 20 s long representative brain electrical activities recorded from subject #8 (channel Cz) during sleep stages NREM4, NREM2 and REM can be seen in Fig. 1. Due to the transient zone at the low end of the plot we set a low cut-off point as well. The low cut-off point (lcf = 50) was ~ 20 % of N/K. Thus, we used only values of n that lie between the low and high cut-off points to estimate H. This range of n (lcf~ 0.2 s, hcf ~ 1 s) was in agreement with the scaling range [0.2 s 1 s] used for estimation of DFAα-exponents in (Shen et al., 2003). Hereby our estimations were not influenced by the frequency cut-offs of the applied 0.3–70 Hz or (3.333 s)−1 to (0.014 s)−1 band-pass filter.
2.2.3. Estimation of dDUsing the Alfréd Rényi’s generalized entropy, a continuous spectrum of generalized dimensions (also called Rényi dimensions or fractal spectrum) Dq can be defined, where −∞≤q≤∞ (Rényi, 1971). A common method for estimation of fractal spectra is the box-counting technique. In this study we applied a box-counting approach that is based on estimation of the moments of signal amplitude distribution and was also used in (Kulish et al., 2006). In this case Dq is defined as follows:
8δV is the bin width or box length (set to 0.3μV based on the conversion range and the resolution of the analogue to digital converter). The partition function can be obtained using
where b(8δV) denotes the number of non-overlapping bins
Vmax and Vmin are the maximum and minimum values of EEG signals recorded during measurements, respectively. χi(q, 8δV) = piq is a weighted measure that represents the percentage of EEG values that falls into the ith bin, and q is the moment or weight of the measure. If ni is the number of EEG values in the ith bin and N is the total number of the samples, than the probability that the signal falls into the ith bin of length 8δV is:
Some of the Dq values are known under different names and widely used in the field of time series analysis. D0 is the Hausdorff–Besicovitch or fractal dimension. For q = 1 one should use
where the numerator is the well-known Shannon’s entropy. D2 is called correlation dimension. The range of fractal spectra is defined as dD=max(Dq)−min(Dq), where max(Dq)=D−∞, min(Dq)=D∞, i.e., dD=D−∞ −D∞, since Dq is a monotonically decreasing function. dD is a measure of multifractality, indicates deviation from monofractal. Larger dD indicates multifractality,while smaller dD indicates that the analyzed system tends to possess themonofractal property.We estimated the range values by dD=D−50 −D50 based on preliminary analysis (Fig. 1). 2.2.4. Post-processingWe performed trend analysis applying a moving average on H and dD values that were estimated for the whole-night recordings to emphasize slower dynamics and suppress promiscuous perturbations that can occur due to artefacts. Moving average of the X(i) discrete time series with a 2a +1, a =1, 2,… long sliding window was defined as:
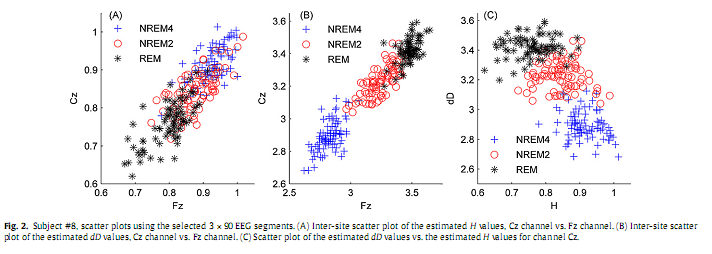
The value of parameter a was set to 45 for visualization purposes, depicting this way averages of 91 estimated values of H and dD. 2.2.5. Statistical analysisTo test whether the dependent variables H and dD are both together affected by the sleep stages, first we performed one-way multivariate analysis of variance (MANOVA). The independent variable “STAGE” contained groups NREM4, NREM2 and REM. Afterwards, to identify the specific dependent variables that contributed to the significant overall effect, one-way ANOVA test was applied to both dependent variables (H and dD). Since ANOVA revealed significant main effects for both H and dD, Tukey HSD post hoc test was used for pairwise comparison of group means. All statistical tests were carried out both at the individual and the group level and for all channels separately. At the individual level comparison between sleep stages relied on the selected 3×90 epochs of 20 s length, while at the group level comparison was based on the individual averages. Calculation of inter-site correlation of both H and dD measures as well as cross-correlation between H and dD was based on 20 s epochs (with 19 s overlap) in the whole-night recordings of each individual. For these calculations awake data segments containing artefacts were trimmed from the beginning and the end of the whole-night recordings. At the group level correlations were calculated using all the 10×3×90 selected 20 s long segments. Visual observation of scatter plots revealed linear inter-site correlations of both measures (Fig. 2A and B). Therefore, to calculate inter-site correlations Pearson’s linear correlation coefficient (rP) was estimated for all 153 pairs of electrodes and for both H and dD. Due to the lack of linearity in the H vs. dD scatter plots (Fig. 2C) Spearman’s rank correlation test (estimation of the rS coefficient) was applied for all electrodes to assess the cross-correlation between H and dD. The applied statistical test are described in almost all textbooks of statistics, here we refer to (Sheskin, 2004).
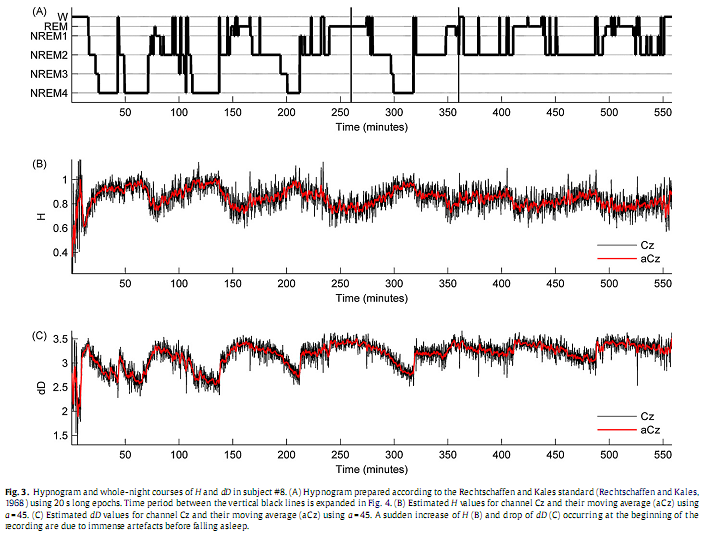
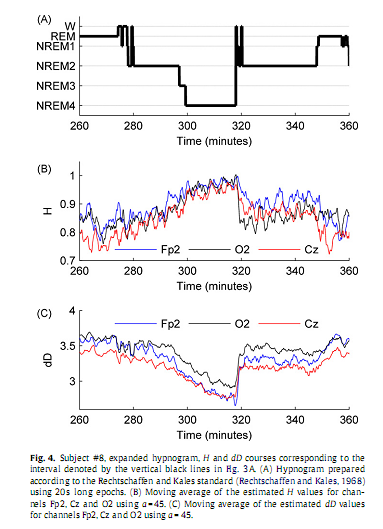
3. Results3.1. Individual analysisSince results found at the individual level were near similar across subjects here we restrict presentation of individual data to a representative subject (#8). Inspection of individual whole-night H and dD profiles and corresponding hypnograms in this subject indicated a visually striking correlation with the succession of sleep cycles. As can be seen in Fig. 3, as sleep deepens H increases and dD decreases while with sleep shallowing H and dD exhibit an inverse course. In Fig. 4, H and dD measures are shown with an expanded time scale for a single sleep cycle that contains a typical sequence of sleep stages and for three EEG channels to picture the variation of H and dD across brain regions and vigilance states.
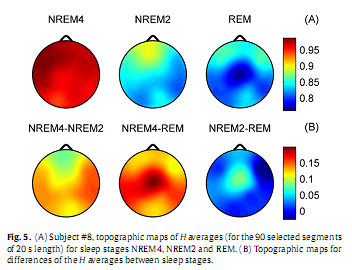
One-way MANOVA analysis yielded a statistically significant overall effect for all channels (Wilks’ λ = 0.05–0.08; F4,532 = 340.04–437.82; p <0.00001). Subsequent one-way ANOVA tests revealed statistically significant main effects for both measures in all channels (p <0.00001) Fig. 5A depicts the topography of average H (for the selected 90 segments) for the three vigilance states. Highest average H values emerged in the frontal region during all vigilance states, while the minimum was found during REM in the central zone. A HNREM4 >HNREM2 >HREM trend could be observed across the whole head surface. Post hoc tests revealed significant differences between stages NREM4 and NREM2 aswell as between NREM4 and REM in all channels (p < 0.0001). Comparison of NREM2 and REM stages reached significancy at the following recording sites only: Fp1, Fp2, F3, Fz, F4, C3, Cz, C4 and P3 (p < 0.0001); T3 (p < 0.001); T5 (p < 0.01). Difference between NREM4 and REM as well as between NREM2 and REM reached maxima in Cz electrode (Fig. 5B).
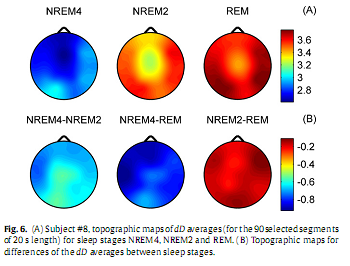
Measure dD, as expected based on the inverse course of H and dD, showed an opposite trend between sleep stages: dDREM > dDNREM2 > dDNREM4 (Fig. 6A). During all sleep stages minima of dD could be found in the fronto-central region. The central difference peak that was present for H (Fig. 5B) disappeared in the dD difference maps (Fig. 6B). Multiple comparisons revealed significant dD differences (p < 0.0001) for all sleep stage pairs in all channels.
3.2. Analysis at the group level
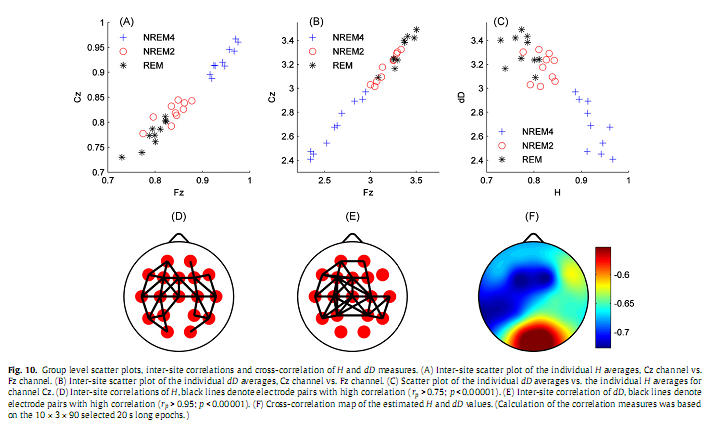
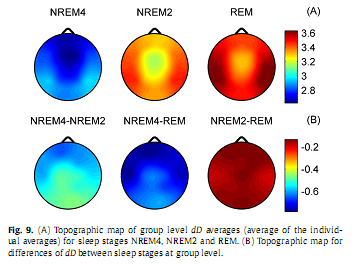
Overall, group level results for H (Fig. 8) were similar to those obtained for subject #8 (Fig. 5). Higher values of H predominated in the frontal region during all sleep stages while the minimum was found in central electrodes during REM. Significant differences (p < 0.001) of H were found between stages NREM4 and NREM2 as well as between NREM4 and REM in all channels. Difference of H between NREM2 and REM stages was significant in the midline electrodes Fz, Cz (p < 0.01) and C3 electrode (p < 0.05) only. Group level dD results are depicted in Fig. 9. Averages of the individual dD averages and their differences between sleep stages were similar to those results obtained for subject #8 (Fig. 6). Comparisons revealed significant dD differences (p < 0.001) between stages NREM4 and NREM2 as well as between NREM4 and REM at all recording sites. Measure dD also tended to be smaller during NREM2 compared to REM but this difference reached significancy (p < 0.05) in channels T3, T4 and C3 only. Inter-site correlation and cross-correlation analyses revealed similar results at the group level (Fig. 10) as for subject #8 (Fig. 7). Significant (p <0.00001) inter-site correlations were found for all channel pairs for both H and dD (H: 0.51≤ rP ≤ 0.91; dD: 0.86 ≤ rP ≤ 0.97). Correlation measure rP peaked for neighbouring channels (Fig. 10D and E). Measure dD exhibited higher inter-site correlations and showed a slightly different topography compared to that of H. Strong negative cross-correlation was found between H and dD for all electrodes (−0.73 ≤ rS ≤ −0.55; p <0.00001) peaking at F3 recording site and having a nadir in the occipital region (Fig. 10F). 4. DiscussionIn the present study, we used fractal properties to describe spatial and temporal dynamics of brain electrical activities during sleep. As far as we know, this is the first study evaluating MOF and MUF properties of the sleep EEG recorded with multiple scalp electrodes. Our results revealed a significant influence of both sleep stages and topography on temporal fractal properties of the human EEG. The MUF measure dD showed a negative, while the MOF measure H exhibited a positive correlation with the depth of the sleep. This indicates that EEG signals tend to be less multifractal and have longer memory properties during NREM4 compared to NREM2 and REM sleep stages. The only study (Acharya et al., 2005) that assessed the H parameter failed to reveal such relationship with sleep depth. Other studies (Shen et al., 2003; Lee et al., 2004; Leistedt et al., 2007a,b), however, described a relation of sleep depth with the DFA exponent α, a parameter linearly related to H (Kantz and Schreiber, 2003). In (Ma et al., 2006), using the same database of EEG recordings sampled with 100 Hz as used in (Acharya et al., 2005), the range of the singularity strength showed a trend opposite to that found for measure dD in this study. Difference between our results and some of the previous data (Acharya et al., 2005; Ma et al., 2006) might be due to difference in the sampling rate and might be interpreted as speaking in favour of higher sampling rates for the estimation of MOF and MUF measures. These discrepancies indicate a need for a comprehensive comparison of different approaches used for the assessment of fractal properties, including classification of EEG signals into one of two classes of fractional time series (fractional Gaussian noise and fractional Brownian motion) as it was proposed in (Eke et al., 2000).
Because of the already mentioned doubts related to estimation of nonlinear measures from time series of finite length, it is more reasonable to assess the variance of the estimated measures across different sleep stages than to find a theoretical relationship between specific estimated values and states of underlying dynamical systems. In the present study significant differences were unveiled for both H and dD between sleep stages NREM4 and NREM 2 as well as between NREM4 and REM in all electrodes. At the group level differences of H and dD between NREM2 and REM were significant at circumscribed regions only. Largest H differences between sleep stages emerged in fronto-central electrodes indicating higher discriminative power of this region. Although dD showed a strong negative correlation with H at each recording site, a slightly different spatial distribution emerged in their inter-site correlationmaps, indicating that the human sleep EEG is more complex than it could be described by a single MOF parameter and that MUF measures are also needed for precise characterization of the fractal behaviour of these signals. The negative cross-correlation between H and dD is in agreement with those results presented by Pereda et al. (1998) (negative correlation between the fractal exponent β and the correlation dimension) and by Shen et al. (2003) (negative correlation between the DFA exponent α and the dimensional complexity). Nevertheless, the particular electrophysiological determinants of the cross-correlation topography (fronto-central peak and occipital nadir) should be revealed using sleep stage level cross-correlation analyses. Due to immense artefacts, waking could not be assessed reliably in the present study. However, visual inspection of artefact-free epochs before falling asleep and following morning awakenings indicated that in these epochs H tended to be smaller while dD seemed to be higher than during sleep. Since waking scalp EEG is intermixed with almost-continuous artefacts, application of additional artefact removal methods and/or intracranial recordings are needed to statistically describe fractal properties of the waking EEG. Although in the present study we did not directly compare fractal properties with spectral components it seems likely that most of the variability of H could be explained by the presence of slow oscillations. This assumption is supported by the facts that highest H values were found during NREM4, a stage characterized by the predominance of slow (~ 1 Hz) activity and that during NREM4 and NREM2 highest H values were located frontally (Figs. 5A and 8A) in accordance with the known frontal predominance of slow wave activity during NREM sleep (Massimini et al., 2004; Tinguely et al., 2006). In addition, individual whole-night H curves indicate a declining trend across the night (Fig. 3B). Such a trend is in accordance with the known decline in slow wave activity across the night, a phenomenon also recognized as a marker for the decrease of the homeostatic Process Swithin the two-processmodel of sleep homeostasis. This model postulates that sleep is regulated in a homeostatic manner and Process S increases as an exponential saturating function during waking and decreases as an exponential function during sleep (Borbély, 1982; Achermann, 2004). In the present study REM could also be characterized by frontal peaks of H. However, we cannot exclude that high frontal H values during REM result from eye movements. Although those epochs with large amplitude rapid eyemovements superimposed on EEG channels were not included in the statistical analysis, itwas not possible to completely exclude these kinds of artefacts. Yet it has to be noted that such a preferential selectionmight introduce a bias towards the selection of tonic REM at the expense of phasic REM epochs and a bias in the quantification of fractal measures of the EEG. Lower H values during REM compared with NREM could be explained by a shift from slow (~ 1 Hz) activity toward lower amplitude higher frequency activities such as saw tooth waves. Since saw tooth wave activity is known to exhibit a central maximum (Yasoshima et al., 1984) this might also explain the observed central nadir of H. Low frontal levels of dD during NREM4 and NREM2 (Figs. 5A and 7A) are in agreement with the observed negative cross-correlation between H and dD. During REM, however, the central nadir of dD does not fit into this tendency since H also exhibited a nadir centrally during this state. Since dD reflects uniformity of amplitude distribution we speculate that the observed central dD nadir might be due to the central predominance of saw tooth waves contributing tomore even amplitude distribution at this recording site. A similar assumption might explain the centralminimum of dD during NREM2 given the well-known vertex peak in sleep spindle activity (De Gennaro and Ferrara, 2003). At the same time the topography of H during NREM2 does not show a central nadir that should be expected based on central drop of H during REM as well as central drops of dD during REM and NREM2. This might be due to the frontal and central predominance of K-complexes (Halasz, 2005) which as being high amplitude low frequency graphoelements contribute to higher H values at these recording sites. The fronto-central predominance of K-complexes during NREM2 might also explain higher power of Fz and Cz electrodes in discriminating NREM2 and REM using H. These results are in agreement with those presented in (Shen et al., 2003) where significantly different correlation was found between the dimensional complexity and the DFA exponent λ during NREM2A (segments containing sharp waves larger than 100 μV) compared to NREM2B (segments with only small or no sharp waves) sleep. Nevertheless, correlation of H and dD measures with spectral components should be assessed in a spatio-temporal manner to verify these assumptions. Results obtained in the present study might have implications for different application areas. For example, combination of H and dD measures with other usual linear and nonlinear descriptors might improve performance of automatic and semi-automatic methods for sleep stage classification. Topographic data presented in this study might also contribute to the selection of most appropriate EEG channels for this purpose. In the field of epilepsy research different measures have been tested for detection and prediction of seizures. Nevertheless, an algorithm with sufficient sensitivity and specificity has not yet been developed for prediction (Mormann et al., 2006; Lehnertz et al., 2007). One of the likely reasons is that the well-known seizure precipitating influence of vigilance states (Mendez and Radtke, 2001) was not considered in most of these studies. Recent studies (Navarro et al., 2005; Schelter et al., 2006; Bruzzo et al., 2008) also suggested that the sleep–wake cycle contribute to limits of specificity of the analyzed measures, but the influence of the vigilance state and the electrode position on the applied measures has not yet been assessed using healthy sleep EEG recordings. In a preliminary study (Weiss et al., 2008a,b) gradual changes of H and dD parameters were found in intracranial EEG recordings during intervals preceding epileptic seizures. Due to the lack of polygraphic and extracranial scalp electrodes in those studies it was not possible to assess the influence of vigilance states. In the present study we reveal robust influence of sleep depth on fractal properties of the sleep EEG. It remains to be clarified whether fractal properties of the EEG are able to predict seizures independently of the predictive value of the sleep stages themselves. These results might promote a comprehensive assessment of correlations between the nonlinear measures used for prediction of epileptic seizures and vigilance states as well as their comparison with appropriate linear measures using surrogate data testing. AcknowledgementsThe authors thank Dr. György Karmos and Dr. Tamás Roska for their helpful comments. This research was supported by the Hungarian Molecular Biology and Info-bionics in Medical Research Grant: RET—05/2004, OMFB—01426/2004. Appendix A. Supplementary dataSupplementary data associatedwith this article can be found, in the online version, at doi:10.1016/j.jneumeth.2009.07.027. ReferencesAcharya R, Faust O, Kannathal N, Chua T, Laxminarayan S. Non-linear analysis of EEG signals at various sleep stages. Comput Methods Programs Biomed 2005;80:37–45. Achermann P. The two-processmodel of sleep regulation revisited. Aviat Space Environ Med 2004;75:A37–43. Beran J. Statistics for Long-Memory Processes. 1st ed. New York: Chapman & Hall/CRC; 1994. Borbély A. A two processmodel of sleep regulation.HumNeurobiol 1982;1:195–204. Bruzzo A, Gesierich B, Santi M, Tassinari C, Birbaumer N, Rubboli G. Permutation entropy to detect vigilance changes and preictal states fromscalp EEG in epileptic patients. A preliminary study. Neurol Sci 2008;29:3–9. DeGennaro L, FerraraM. Sleep spindles: an overview. SleepMed Rev 2003;7:423–40. Eke A, Hermán P, Bassingthwaighte J, Raymond G, Percival D, Cannon M, et al. Physiological time series: distinguishing fractal noises from motions. Pflugers Arch 2000; 439:403–15. Halasz P. K-complex, a reactive EEG graphoelement of NREM sleep: an old chap in a new garment. Sleep Med Rev 2005;9:391–412. Hu K, Ivanov P, Chen Z, Carpena P, Stanley H. Effect of trends on detrended fluctuation analysis. Phys Rev E Stat Nonlin Soft Matter Phys 2001;64:011114. Jestczemski F, Sernetz M. Multifractal approach to inhomogeneous fractals. Phys A 1996;223:275–82. Kantz H, Schreiber T. Nonlinear time series analysis. 2nd ed. Cambridge/New York/Melbourne: Cambridge University Press; 2003. Kiselev VG, Hahn KR, Auer DP. Is the brain cortex a fractal? Neuroimage 2003;20:1765–74. Kulish V, Sourin A, Sourina O. Human electroencephalograms seen as fractal time series: mathematical analysis and visualization. Comput Biol Med 2006;36:291–302. Lee JM, KimDJ, KimIY, Park KS, KimSI. Nonlinear-analysis of human sleep EEG using detrended fluctuation analysis. Med Eng Phys 2004;26:773–6. Lehnertz K, Mormann F, Osterhage H, Muller A, Prusseit J, Chernihovskyi A, et al. State-of-the-art of seizure prediction. J Clin Neurophysiol 2007;24:147–53. Leistedt S, Dumont M, Coumans N, Lanquart J, Jurysta F, Linkowski P. The modifications of the long-range temporal correlations of the sleep EEG due to major depressive episode disappear with the status of remission. Neuroscience 2007a;148:782–93. Leistedt S, Dumont M, Lanquart JP, Jurysta F, Linkowski P. Characterization of the sleep EEG in acutely depressed men using detrended fluctuation analysis. Clin Neurophysiol 2007b;118:940–50. Lewis CD, Gebber GL, Larsen PD, Barman SM. Long-term correlations in the spike trains of medullary sympathetic neurons. J Neurophysiol 2001;85:1614–22. Lowen SB, Liebovitch LS, White JA. Fractal ion-channel behavior generates fractal firing patterns in neuronal models. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Top 1999;59:5970–80 Ma QL, Ning XB, Wang J, Bian CH. A new measure to characterize multifractality of sleep electroencephalogram. Chin Sci Bull 2006;51:3059–64. Mandelbrot BB. The fractal geometry of nature. 1st ed. NewYork:W.H. Freeman and Company; 1982. Mandelbrot BB, Taqqu MS. Robust R/S analysis of long-run serial correlation. In: Proceedings of the 42nd session of the international statistical institute; 1979. p. 69–104. Massimini M, Huber R, Ferrarelli F, Hill S, Tononi G. The sleep slow oscillation as a traveling wave. J Neurosci 2004;24:6862–70. Mendez M, Radtke R. Interactions between sleep and epilepsy. J Clin Neurophysiol 2001;18:106–27. Mormann F, Elger CE, Lehnertz K. Seizure anticipation: from algorithms to clinical practice. Curr Opin Neurol 2006;19:187–93. Navarro V, Martinerie J, Le Van Quyen M, Baulac M, Dubeau F, Gotman J. Seizure anticipation: do mathematical measures correlate with video-EEG evaluation? Epilepsia 2005;46:385–96. Osorio I, Frei MG. Hurst parameter estimation for epileptic seizure detection. Commun Inf Syst 2007;7:167–76. Pellionisz A. Neural geometry: towards a fractal model of neurons. In: Cotterill RMJ, editor. Models of brain function. Cambridge/New York/Melbourne: Cambridge University Press; 1989. p. 453–64. Pereda E, Gamundi A, Rial R, González J. Non-linear behaviour of human EEG: fractal exponent versus correlation dimension in awake and sleep stages. Neurosci Lett 1998;250:91–4. Rechtschaffen A, Kales A. Amanual of standardized terminology. In: techniques and scoring system for sleep stages of human subjects. Bethesda, MD: U.S. National Institute of Neurological Diseases and Blindness, Neurological Information Network; 1968. Rényi A. Probability theory. North Holland: Amsterdam; 1971. Schelter B, Winterhalder M, Maiwald T, Brandt A, Schad A, Timmer J, et al. Do false predictions of seizures depend on the state of vigilance? A report from two seizure-prediction methods and proposed remedies. Epilepsia 2006;47:2058–70. Shen Y, Olbrich E, Achermann P, Meier PF. Dimensional complexity and spectral properties of the human sleep EEG. Clin Neurophysiol 2003;114:199–209. Sheskin DJ. The handbook of parametric and nonparametric statistical procedures. 3rd ed. Boca Raton, FL: Chapman & Hall/CRC; 2004. Spasic S, Kalauzi A, Grbic G, Martac L, Culic M. Fractal analysis of rat brain activity after injury. Med Biol Eng Comput 2005;43:345–8. StamC. Nonlinear dynamical analysis of EEG andMEG: review of an emerging field. Clin Neurophysiol 2005;116:2266–301. Tel T, Vicsek T. Geometrical multifractality of growing structures. J Phys AMath Gen 1987;20:L835–40. Tinguely G, Finelli LA, Landolt HP, Borbely AA, Achermann P. Functional EEG topography in sleep and waking: state-dependent and state-independent features. Neuroimage 2006;32:283–92. Weiss B,Hegedűs B, Vágó Z, Roska T. Fractal spectra of intracranial electroencephalograms in different types of epilepsy. In: 19th international EURASIP conference biosignal; 2008a. p. 1–5. Weiss B, Vágó Z, Tetzlaff R, Roska T. Long-range dependence of long-term continuous intracranial electroencephalograms for detection and prediction of epileptic seizures. In: International symposium on nonlinear theory and its applications; 2008b. p. 704–7. Yasoshima A, Hayashi H, Iijima S, Sugita Y, Teshima Y, Shimizu T, et al. Potential distribution of vertex sharpwave and saw-toothed wave on the scalp. Electroencephalogr Clin Neurophysiol 1984;58:73–6
|
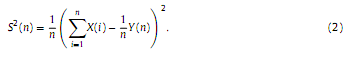
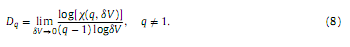
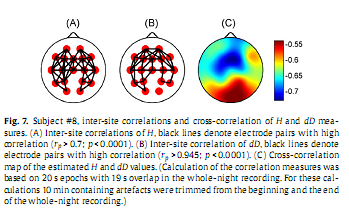Calculating inter-site correlations across the whole sleep period revealed significant (p < 0.0001) inter-site correlations for all channel pairs for both H and dD (H: 0.51 ≤ rP ≤ 0.93; dD: 0.89 ≤ rP ≤ 0.97), however, as expected, correlation measures peaked for neighbouring channels (Fig. 7A and B). When comparing the topography of inter-site correlation maps constructed for the two fractal measures we observed that dD exhibited higher inter-site correlations and showed a slightly different topography compared to that of H (see Supplementary material). Calculating cross-correlation between H and dD measures revealed a strong negative cross-correlation for all electrodes (−0.73≤ rS ≤−0.53; p < 0.0001) peaking at Fz recording site and having a nadir in the occipital region (Fig. 7C).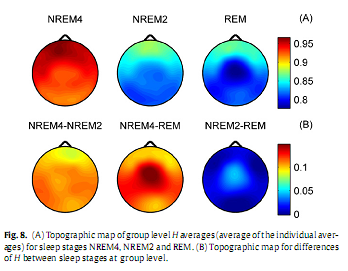
At the group level one-way MANOVA analysis yielded a statistically significant overall effect for all channels (Wilks’ λ = 0.09–0.24; F4,52 = 13.7–30.87; p <0.00001). Subsequent one-way ANOVA tests revealed statistically significant main effects for both measures in all channels (p <0.00001).